。。。翻到原来的提交纪录，发现这题随意打了个高精度就交了。然后心一横决定添了这个坑＝ ＝

题目地址:http://www.lydsy.com/JudgeOnline/problem.php?id=1002

updateNo1: [current time Aug. 1 21:42:36] 找到vfleaking 's blog, 研究 周冬《生成树的计数及其应用》ing。。。

updateNo2: [current time Aug.1 22:50:55] 第一次试图证明Matrix-tree,but failed。。。

updateNo3: [current time Aug.2 22:19:05] 南湖游船上吹着湖风想着行列式，格外的凉爽。。。还是有一点成就的，最起码懂得了行列式怎么算只会2阶和3阶有毛线用。证明略这三个字真是煎熬啊。。。

贴上2阶3阶行列式计算公式：

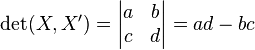
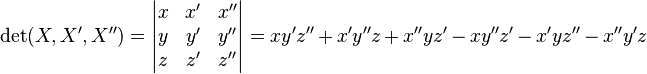
update_final: [current time Aug.4 0:34:38]放弃证明Matrix-tree，退一步海阔天空[kidding me?],但是成功看懂了kirchoff矩阵化成本题的递推式的一个证明。

其实并不是很难。。。建议稍微看看行列式的基本性质和算法，推荐线代启示录。

首先你应该先明白kirchoff矩阵是什么东西。。。它的其中一个定义是无向图的关联矩阵与该矩阵的转置矩阵的乘积，但其实也可以定义为图的点度数矩阵D-它的临接矩阵A，显然，kirchoff 矩阵C满足当i=j时，C_ij 为点V_i的度数，而当i != j时，若存在边(Vi,Vj)，那么C_ij=-1，否则为0。

接下来可以引入Matrix-tree定理(important!)：对于一个无向图G，生成树的个数等于其kirchoff矩阵的任何一个n-1阶主子式的行列式的绝对值！

回到这题上，我们可以来写写看本题的图的kirchoff矩阵(删去中间的点的n-1阶主子式)，大概是这样的：

然后,对于这个矩阵进行一些变换，可以得到一个上三角行列式，其中有一些数是关于n的递推式，由此，可以推出一个十分不错的结论：f[n]=3*f[n-1]-f[n-2]（论怎样把一道矩阵题变为高精度练习。。），计算该行列式的详细步骤还是ym一下VFleaKing大神。。。

N久前还是不知情况的大众时写的代码,还是不贴为好。。。

Orz  智商被碾压。。。

Fractal128